
Chuyển đổi hệ thập phân sang hệ nhị phân và ngược lại
Hướng dẫn cách chuyển đổi giữa hệ nhị phân sang hệ thập phân và ngược lại hệ thập phân sang hệ nhị phân.
- Hệ số thập phân (
decimalhay còn gọi là hệ đếm cơ số 10) có mười giá trị (0,1,2,3,4,5,6,7,8,9) cho từng trị số. - Hệ nhị phân (
binaryhay còn gọi là hệ đếm cơ số 2) là một hệ đếm chỉ dùng hai ký tự là 0 và 1để biểu đạt một giá trị số. Và bạn cũng có các phép toán cơ bản cộng, trừ, nhân, chia trên hệ nhị phân. Trong bài này tôi sẽ trình bài cách chuyển đổi qua lại giữa hệ nhị phân và hệ thập phân.
Chuyển hệ thập phân sang hệ nhị phân
Nguyên tắc của phương pháp này là lấy số cần chuyển đổi chia cho 2 (kết quả chỉ lấy phần nguyên), sau đó tiếp tục lấy kết quả chia cho 2 (và cũng chỉ lấy phần nguyên), kết quả số nhị phân thu được là tập hợp các số dư của các phép chia (lấy từ phép chia cuối cùng trở lên trên). Để dễ hình dung ta sẽ làm các ví dụ sau:
Ví dụ 1: Chuyển số 30 sang hệ nhị phân
30/2 = 15 (dư 0) 15/2 = 7 (dư 1) 7/2 = 3 (dư 1) 3/2 = 1 (dư 1) 1/2 = 0 (dư 1)Như vậy, số 30 trong hệ nhị phân sẽ là: 1 1 1 1 0
Ví dụ 2: Chuyển số 71 sang hệ nhị phân
71/2 = 35 (dư 1) 35/2 = 17 (dư 1) 17/2 = 8 (dư 1) 8/2 = 4 (dư 0) 4/2 = 2 (dư 0) 2/2 = 1 (dư 0) 1/2 = 0 (dư 1)Như vậy, số 71 trong hệ nhị phân sẽ là: 1 0 0 0 1 1 1
Ví dụ 3: Chuyển số 0.625 sang hệ nhị phân
- 0.625 x 2=1.25 (lấy số 1), phần lẻ 0.25
- 0.25 x 2=0.5 (lấy số 0), phần lẻ 0.5
- 0.5 x 2=1.0 (lấy số 1), phần lẻ 0.
- Kết thúc phép chuyển đổi, ta thu được kết quả là 1012 (lấy từ phép nhân đầu tiên đến phép nhân cuối cùng)
Ví dụ 4: Chuyển số 9.625 sang hệ nhị phân
- Phần nguyên 9 ta chuyển đổi sang hệ nhị phân là 10012 (đổi tương tự như ví dụ 1 và ví dụ 2)
- Phần lẻ 0.625 đổi sang hệ nhị phân là 101
- Vậy số 9.625 khi đổi sang hệ nhị phân sẽ là 10011012
Chuyển hệ nhị phân sang hệ thập phân
Ví dụ 5: Chuyển đổi số nhị phân 10001112 sang số thập phân.
Ta thấy số 10001112 có tổng cộng 7 kí tự, chúng ta sẽ đánh số 7 kí tự này theo vị trí từ phải sang trái và bắt đầu từ 0 như sau:
| Kí tự nhị phân | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| Vị trí | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Kết quả | 1x26 | 0x25 | 0x24 | 0x23 | 1x22 | 1x21 | 1x20 |
Số thập phân cần tìm là kết quả tổng của kí tự nhị phân x 2 lũy thừa vị trí.
Tức là: (1 x 26)+(0 x 25)+(0 x 24)+(0 x 23)+(1 x 22)+(1 x 21)+(1 x 20). Vậy ta được kết quả là 64+0+0+0+4+2+1=71
Ví dụ 6: Chuyển đổi số nhị phân 111102 sang số thập phân.
Tương tự như ví dụ 5. Ta có bảng sau:
| Kí tự nhị phân | 1 | 1 | 1 | 1 | 0 |
|---|---|---|---|---|---|
| Vị trí | 4 | 3 | 2 | 1 | 0 |
| Kết quả | 1x24 | 1x23 | 1x22 | 1x21 | 0x20 |
Ta được: (1 x 24)+(1 x 23)+(1 x 22)+(1 x 21)+(0 x 20). Vậy ta được kết quả là 16+8+4+2+0=30
hai lần so với khi ở vị trí cũ.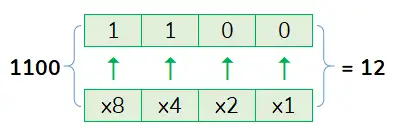
-
- Ví dụ 1: 1102 → 1x4+1x2+0x1=6
- Ví dụ 2: 111102 → 1x16+1x8+1x4+1x2+0x1=30
Như vậy, đó là các cách mà bạn sẽ sử dụng để chuyển đổi hệ cơ số học. Hy vọng bài viết này sẽ giúp bạn phần nào trên con đường tự học của mình.








